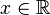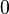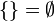1.2 La recta numerica y concepto de intervalo1.2 LA RECTA NUMERICA
La recta numérica, inventada por John Wallis, es un dibujo unidimensional de una línea en la que los números enteros son mostrados como puntos especialmente marcados espaciados uniformemente. Aunque la imagen de abajo muestra solamente los números enteros a entre -9 y 9, la recta incluye todos los números reales, continuando "ilimitadamente" en cada dirección. Frecuente es usada como ayuda para enseñar la adición y la sustracción simples, implicando especialmente números negativos. Está dividida en dos mitades simétricas por el origen, es decir el número cero
. En la recta numérica mostrada arriba, los números negativos se representan en rojo y los positivos en azul.
La recta numérica es más frecuentemente representada horizontalmente. Por costumbre, los números positivos se encuentran del lado derecho del cero y los números negativos de lado izquierdo. Unas flechas en los extremos de la recta sugieren que la línea continúa indefinidamente en las direcciones positivas y negativas, aunque no lo hacen en el papel, la pizarra, o la pantalla. El conjunto de todos los números en la recta numérica también se conoce como el sistema de los números reales, denotado por Los números reales consisten en los números irracional y racionales, así como los números enteros, y los números naturales para contar. Otra recta dibujada perpendicularmente sobre el origen de la primera puede ser usada para representar los números imaginarios. Esto extiende la recta numérica a un plano complejo, con los puntos del plano que representan número complejo números complejos. En análisis, se denomina intervalo a todo subconjunto conexo de la recta real. Más precisamente, son las únicas partes I de R que verifican la siguiente propiedad:
Para representar intervalos, usan habitualmente dos notaciones, por ejemplo, para representar el conjunto de los x tal que a ≤ x < b se puede representar [a; b) o bien [a; b] . La primera es la vigente en el mundo anglosajón, la segunda en Francia y en la francofonía. La regla del corchete invertido resulta más intuitiva si uno se imagina que el corchete es una mano que tira hacia fuera o empuja hacia dentro, respectivamente, un extremo del intervalo. En el ejemplo anterior, a pertenece al intervalo mientras que b no. Es un conjunto de números que se corresponden con los puntos de una recta o segmento, en el que se encuentra un ordenamiento interno entre ellos. Los intervalos es el espacio que se da de un punto a otro en el cual se toman en cuenta todos lo puntos intermedios. Por ejemplo: en una recta tenemos un intervalo:[-2,2]entre este espacio se encuentran los números (-2-1,0,1,2) aquí se encuentra un intervalo.....ya que el espacio abarca una serie de números consecutivos que se corresponden entre sí.
Clasificación [editar]Se pueden clasificar los intervalos según sus características topológicas (intervalos abiertos, cerrados y semi abiertos) o según sus características métricas (su longitud: nula, finita no nula, o infinita). Aquí están todos los casos posibles, con a ≤ b, y x perteneciente al intervalo, y l su longitud:
Si I = ]a, b[, su centro es c = (a + b)/2, y su radio es r = (b - a)/2. a < x < b equivale a |x - c| < r; y se interpreta como la distancia entre x y c es menor que r; se nota x ε B (c, r); B para bola abierta, término que se generaliza a cualquier espacio métrico. De la misma manera, I = [a, b] corresponde a la condición |x - c| ≤ r. En tal caso se habla de bola cerrada. Se nota este conjunto: _ B (c, r) = { x ε R, |x - c| ≤ r }. Es la clausura topológica de la bola abierta B (c, r) = { x ε R, |x - c| < r }. Cuando dos variables - pongamos x e y - toman sus valores en sendos intervalos I e J, es legítimo preguntarse en que intervalo varían su suma, su diferencia, su producto y su cociente. Contestar a esta pregunto permitirá definir las cuatro operaciones sobre los intervalos. Tomemos I = [a, b] y J = [c, d]. Entonces a ≤ x ≤ b, y c ≤ y ≤ d. podemos sumar las inegualdades: a + c ≤ x + y ≤ b + d. Lo que justifica que I + J = [ a + c , b + d ]. Para la diferencia, hay que mirar primero - y : - d ≤ - y ≤ - c, y luego se puede sumar las inegualdades: a - d ≤ x - y ≤ b - c. De ahí obtenemos I - J = [ a - d, b - c ]. Si se toman a, b, c y d positivos no nulos, el producto y el cociente son también sencillos: I · J = [ ac, bd ] y I / J = [ a/d, b/c ]. |
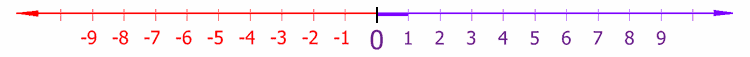

![[a, b] ,](http://upload.wikimedia.org/math/7/f/3/7f3408c72246eece3d5542fc853ce417.png)
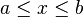
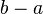

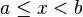
![]a, b] mathrm{ acute o } (a, b] !](http://upload.wikimedia.org/math/0/1/8/0189f84b7a0ea78dbc527c545d8c9598.png)

![]a, b[ mathrm{ acute o } (a, b) !](http://upload.wikimedia.org/math/1/0/d/10d97baef8714cd0982a87681cfe4d1f.png)
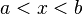
![]-infty, b[ mathrm{ acute o } (- infty, b) !](http://upload.wikimedia.org/math/0/9/7/097e7c70e6cbf2559d82fcb85f853033.png)
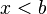

![]-infty, b] mathrm{ acute o } (- infty, b] !](http://upload.wikimedia.org/math/e/8/2/e82cc38f6052cb558df6d0be418c5659.png)
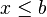
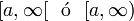
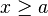
![]a, infty [ mathrm{ acute o } (a, infty ) !](http://upload.wikimedia.org/math/7/6/7/767d79359e390fb402d696537c7d6b24.png)

![]infty, + infty [ mathrm{ acute o } (infty, + infty ) !](http://upload.wikimedia.org/math/6/b/a/6ba8dc9071eaad7acf515f333bba45cf.png)